- 當(dāng)前位置:
- 好師來首頁(yè)
- 學(xué)科首頁(yè)
- 資源預(yù)覽
2018年普通高等學(xué)校招生全國(guó)(Ⅱ)統(tǒng)一考試
理科數(shù)學(xué)
一、選擇題:本題共12小題,每小題5分,共60分.在每小題給出的四個(gè)選項(xiàng)中,只有一項(xiàng)是符合題目要求的.
1.![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.已知集合![]() ,則
,則![]() 中元素的個(gè)數(shù)為
中元素的個(gè)數(shù)為
A.9B.8C.5D.4
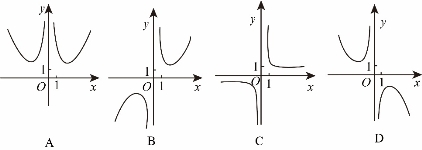
3.函數(shù)![]() 的圖像大致為
的圖像大致為
4.已知向量![]() ,
,![]() 滿足
滿足![]() ,
,![]() ,則
,則![]()
A.4B.3C.2D.0
 5.雙曲線
5.雙曲線![]() 的離心率為
的離心率為![]() ,則其漸近線方程為
,則其漸近線方程為
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.在![]() 中,
中,![]() ,
,![]() ,
,![]() ,則
,則![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
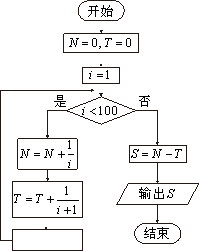
7.為計(jì)算![]() ,設(shè)計(jì)了右側(cè)的程序框圖,則在空白框中應(yīng)填入
,設(shè)計(jì)了右側(cè)的程序框圖,則在空白框中應(yīng)填入
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.我國(guó)數(shù)學(xué)家陳景潤(rùn)在哥德巴赫猜想的研究中取得了世界領(lǐng)先的成果.哥德巴赫猜想是“每個(gè)大于2的偶數(shù)可以表示為兩個(gè)素?cái)?shù)的和”,如![]() .在不超過30的素?cái)?shù)中,隨機(jī)選取兩個(gè)不同的數(shù),其和等于30的概率是
.在不超過30的素?cái)?shù)中,隨機(jī)選取兩個(gè)不同的數(shù),其和等于30的概率是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.在長(zhǎng)方體![]() 中,
中,![]() ,
,![]() ,則異面直線
,則異面直線![]() 與
與![]() 所成角的余弦值為
所成角的余弦值為
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.若![]() 在
在![]() 是減函數(shù),則
是減函數(shù),則![]() 的最大值是
的最大值是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.已知![]() 是定義域?yàn)?/span>
是定義域?yàn)?/span>![]() 的奇函數(shù),滿足
的奇函數(shù),滿足![]() .若
.若![]() ,則
,則![]()
A.![]() B.0C.2D.50
B.0C.2D.50
12.已知![]() ,
,![]() 是橢圓
是橢圓![]() 的左、右焦點(diǎn),
的左、右焦點(diǎn),![]() 是
是![]() 的左頂點(diǎn),點(diǎn)
的左頂點(diǎn),點(diǎn)![]() 在過
在過![]() 且斜率為
且斜率為![]() 的直線上,
的直線上,![]() 為等腰三角形,
為等腰三角形,![]() ,則
,則![]() 的離心率為
的離心率為
A. ![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空題:本題共4小題,每小題5分,共20分.
13.曲線![]() 在點(diǎn)
在點(diǎn)![]() 處的切線方程為__________.
處的切線方程為__________.
14.若![]() 滿足約束條件
滿足約束條件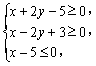 則
則![]() 的最大值為__________.
的最大值為__________.
15.已知![]() ,
,![]() ,則
,則![]() __________.
__________.
16.已知圓錐的頂點(diǎn)為![]() ,母線
,母線![]() ,
,![]() 所成角的余弦值為
所成角的余弦值為![]() ,
,![]() 與圓錐底面所成角為45°,若
與圓錐底面所成角為45°,若![]() 的面積為
的面積為![]() ,則該圓錐的側(cè)面積為__________.
,則該圓錐的側(cè)面積為__________.
三、解答題:共70分。解答應(yīng)寫出文字說明、證明過程或演算步驟。第17~21題為必考題,每個(gè)試題考生都必須作答.第22、23為選考題,考生根據(jù)要求作答.
(一)必考題:共60分。
17.(12分)
記![]() 為等差數(shù)列
為等差數(shù)列![]() 的前
的前![]() 項(xiàng)和,已知
項(xiàng)和,已知![]() ,
,![]() .
.
(1)求![]() 的通項(xiàng)公式;
的通項(xiàng)公式;
(2)求![]() ,并求
,并求![]() 的最小值.
的最小值.
18.(12分)
下圖是某地區(qū)2000年至2016年環(huán)境基礎(chǔ)設(shè)施投資額![]() (單位:億元)的折線圖.
(單位:億元)的折線圖.
 為了預(yù)測(cè)該地區(qū)2018年的環(huán)境基礎(chǔ)設(shè)施投資額,建立了
為了預(yù)測(cè)該地區(qū)2018年的環(huán)境基礎(chǔ)設(shè)施投資額,建立了![]() 與時(shí)間變量
與時(shí)間變量![]() 的兩個(gè)線性回歸模型.根據(jù)2000年至2016年的數(shù)據(jù)(時(shí)間變量
的兩個(gè)線性回歸模型.根據(jù)2000年至2016年的數(shù)據(jù)(時(shí)間變量![]() 的值依次為
的值依次為![]() )建立模型①:
)建立模型①:![]() ;根據(jù)2010年至2016年的數(shù)據(jù)(時(shí)間變量
;根據(jù)2010年至2016年的數(shù)據(jù)(時(shí)間變量![]() 的值依次為
的值依次為![]() )建立模型②:
)建立模型②:![]() .
.
(1)分別利用這兩個(gè)模型,求該地區(qū)2018年的環(huán)境基礎(chǔ)設(shè)施投資額的預(yù)測(cè)值;
(2)你認(rèn)為用哪個(gè)模型得到的預(yù)測(cè)值更可靠?并說明理由.
19.(12分)
設(shè)拋物線![]() 的焦點(diǎn)為
的焦點(diǎn)為![]() ,過
,過![]() 且斜率為
且斜率為![]() 的直線
的直線![]() 與
與![]() 交于
交于![]() ,
,![]() 兩點(diǎn),
兩點(diǎn),![]() .
.
(1)求![]() 的方程
的方程
(2)求過點(diǎn)![]() ,
,![]() 且與
且與![]() 的準(zhǔn)線相切的圓的方程.
的準(zhǔn)線相切的圓的方程.
20.(12分)
如圖,在三棱錐![]() 中,
中,![]() ,
,![]() ,
,![]() 為
為![]() 的中點(diǎn).
的中點(diǎn).
(1)證明:![]() 平面
平面![]() ;
;
(2)若點(diǎn)![]() 在棱
在棱![]() 上,且二面角
上,且二面角![]() 為
為![]() ,求
,求![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.

21.(12分)
已知函數(shù)![]() .
.
(1)若![]() ,證明:當(dāng)
,證明:當(dāng)![]() 時(shí),
時(shí),![]() ;
;
(2)若![]() 在
在![]() 只有一個(gè)零點(diǎn),求
只有一個(gè)零點(diǎn),求![]() .
.
(二)選考題:共10分.請(qǐng)考生在第22、23題中任選一題作答。如果多做,則按所做的第一題計(jì)分.
22.[選修4-4:坐標(biāo)系與參數(shù)方程](10分)
在直角坐標(biāo)系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)),直線
為參數(shù)),直線![]() 的參數(shù)方程為
的參數(shù)方程為
![]() (
(![]() 為參數(shù)).
為參數(shù)).
(1)求![]() 和
和![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)若曲線![]() 截直線
截直線![]() 所得線段的中點(diǎn)坐標(biāo)為
所得線段的中點(diǎn)坐標(biāo)為![]() ,求
,求![]() 的斜率.
的斜率.
23.[選修4-5:不等式選講](10分)
設(shè)函數(shù)![]() .
.
(1)當(dāng)![]() 時(shí),求不等式
時(shí),求不等式![]() 的解集;
的解集;
(2)若![]() ,求
,求![]() 的取值范圍.
的取值范圍.
更多高中數(shù)學(xué)試卷
- 2025年春考必備:2024年上海市春季高考數(shù)學(xué)試卷.docx
- 2024年上海市高考數(shù)學(xué)試卷.doc
- 北京2024高考數(shù)學(xué).docx
- 2018年普通高等學(xué)校招生全國(guó)統(tǒng)一考試文科數(shù)學(xué).docx
- 2018年普通高等學(xué)校招生全國(guó)統(tǒng)一考試數(shù)學(xué)(文)(北京卷).docx
- 2018年普通高等學(xué)校招生全國(guó)統(tǒng)一考試(江蘇卷)數(shù)學(xué)Ⅰ.docx
- 2018年普通高等學(xué)校招生全國(guó)(Ⅱ)統(tǒng)一考試文科數(shù)學(xué).docx
- 2018年普通高等學(xué)校招生全國(guó)統(tǒng)一考試數(shù) 學(xué)(理)(北京卷).docx
- 2018年普通高等學(xué)校招生全國(guó)統(tǒng)一考試?yán)砜茢?shù)學(xué).docx
- 2019年全國(guó)統(tǒng)一高考數(shù)學(xué)試卷(理科)(1卷).docx






