2018年普通高等學校招生全國統一考試
理科數學
一、選擇題:本題共12小題,每小題5分,共60分。在每小題給出的四個選項中,只有一項是符合題目要求的。
1.設![]() ,則
,則![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.已知集合![]() ,則
,則![]()
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.某地區經過一年的新農村建設,農村的經濟收入增加了一倍,實現翻番.為更好地了解該地區農村的經濟收入變化情況,統計了該地區新農村建設前后農村的經濟收入構成比例,得到如下餅圖:
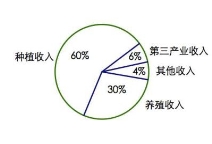
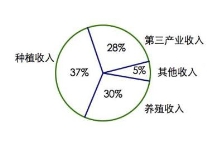
建設前經濟收入構成比例建設后經濟收入構成比例
則下面結論中不正確的是
A.新農村建設后,種植收入減少
B.新農村建設后,其他收入增加了一倍以上
C.新農村建設后,養殖收入增加了一倍
D.新農村建設后,養殖收入與第三產業收入的總和超過了經濟收入的一半
4.記![]() 為等差數列
為等差數列![]() 的前
的前![]() 項和.若
項和.若![]() ,
,![]() ,則
,則![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.設函數![]() .若
.若![]() 為奇函數,則曲線
為奇函數,則曲線![]() 在點
在點![]() 處的切線方程為
處的切線方程為
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.在![]() 中,
中,![]() 為
為![]() 邊上的中線,
邊上的中線,![]() 為
為![]() 的中點,則
的中點,則![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
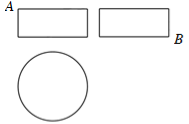
7.某圓柱的高為2,底面周長為16,其三視圖如圖.圓柱表面上的點![]() 在正視圖上的對應點為
在正視圖上的對應點為![]() ,圓柱表面上的點
,圓柱表面上的點![]() 在左視圖上的對應點為
在左視圖上的對應點為![]() ,則在此圓柱側面上,從
,則在此圓柱側面上,從![]() 到
到![]() 的路徑中,最短路徑的長度為
的路徑中,最短路徑的長度為
A.![]() B.
B.![]() C.3D.2
C.3D.2
8.設拋物線C:y2=4x的焦點為F,過點(–2,0)且斜率為![]() 的直線與C交于M,N兩點,則
的直線與C交于M,N兩點,則![]() =
=
A.5B.6C.7D.8
9.已知函數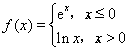
![]() .若g(x)存在2個零點,則a的取值范圍是
.若g(x)存在2個零點,則a的取值范圍是
A.[–1,0)B.[0,+∞)C.[–1,+∞)D.[1,+∞)
10.下圖來自古希臘數學家希波克拉底所研究的幾何圖形.此圖由三個半圓構成,三個半圓的直徑分別為直角三角形ABC的斜邊BC,直角邊AB,AC.![]() 的三邊所圍成的區域記為Ⅰ,黑色部分記為Ⅱ,其余部分記為Ⅲ.在整個圖形中隨機取一點,此點取自Ⅰ,Ⅱ,Ⅲ的概率分別記為p1,p2,p3,則
的三邊所圍成的區域記為Ⅰ,黑色部分記為Ⅱ,其余部分記為Ⅲ.在整個圖形中隨機取一點,此點取自Ⅰ,Ⅱ,Ⅲ的概率分別記為p1,p2,p3,則
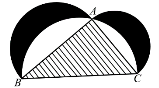
A.p1=p2B.p1=p3
C.p2=p3D.p1=p2+p3
11.已知雙曲線C:![]() ,O為坐標原點,F為C的右焦點,過F的直線與C的兩條漸近線的交點分別為M、N.若
,O為坐標原點,F為C的右焦點,過F的直線與C的兩條漸近線的交點分別為M、N.若![]() 為直角三角形,則|MN|=
為直角三角形,則|MN|=
A.![]() B.3C.
B.3C.![]() D.4
D.4
12.已知正方體的棱長為1,每條棱所在直線與平面α所成的角都相等,則α截此正方體所得截面面積的最大值為
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空題:本題共4小題,每小題5分,共20分。
13.若![]() ,
,![]() 滿足約束條件
滿足約束條件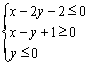 ,則
,則![]() 的最大值為_____________.
的最大值為_____________.
14.記![]() 為數列
為數列![]() 的前
的前![]() 項和.若
項和.若![]() ,則
,則![]() _____________.
_____________.
15.從2位女生,4位男生中選3人參加科技比賽,且至少有1位女生入選,則不同的選法共有_____________種.(用數字填寫答案)
16.已知函數![]() ,則
,則![]() 的最小值是_____________.
的最小值是_____________.
三、解答題:共70分。解答應寫出文字說明、證明過程或演算步驟。第17~21題為必考題,每個試題考生都必須作答。第22、23題為選考題,考生根據要求作答。
(一)必考題:60分。
17.(12分)
在平面四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求![]() ;
;
(2)若![]() ,求
,求![]() .
.
18.(12分)
如圖,四邊形![]() 為正方形,
為正方形,![]() 分別為
分別為![]() 的中點,以
的中點,以![]() 為折痕把
為折痕把![]() 折起,使點
折起,使點![]() 到達點
到達點![]() 的位置,且
的位置,且![]() .
.
(1)證明:平面![]() 平面
平面![]() ;
;
(2)求![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
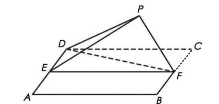
19.(12分)
設橢圓![]() 的右焦點為
的右焦點為![]() ,過
,過![]() 的直線
的直線![]() 與
與![]() 交于
交于![]() 兩點,點
兩點,點![]() 的坐標為
的坐標為![]() .
.
(1)當![]() 與
與![]() 軸垂直時,求直線
軸垂直時,求直線![]() 的方程;
的方程;
(2)設![]() 為坐標原點,證明:
為坐標原點,證明:![]() .
.
20.(12分)
某工廠的某種產品成箱包裝,每箱200件,每一箱產品在交付用戶之前要對產品作檢驗,如檢驗出不合格品,則更換為合格品.檢驗時,先從這箱產品中任取20件作檢驗,再根據檢驗結果決定是否對余下的所有產品作檢驗,設每件產品為不合格品的概率都為![]() ,且各件產品是否為不合格品相互獨立.(1)記20件產品中恰有2件不合格品的概率為
,且各件產品是否為不合格品相互獨立.(1)記20件產品中恰有2件不合格品的概率為![]() ,求
,求![]() 的最大值點
的最大值點![]() .
.
(2)現對一箱產品檢驗了20件,結果恰有2件不合格品,以(1)中確定的![]() 作為
作為![]() 的值.已知每件產品的檢驗費用為2元,若有不合格品進入用戶手中,則工廠要對每件不合格品支付25元的賠償費用.
的值.已知每件產品的檢驗費用為2元,若有不合格品進入用戶手中,則工廠要對每件不合格品支付25元的賠償費用.
(i)若不對該箱余下的產品作檢驗,這一箱產品的檢驗費用與賠償費用的和記為![]() ,求
,求![]() ;
;
(ii)以檢驗費用與賠償費用和的期望值為決策依據,是否該對這箱余下的所有產品作檢驗?
21.(12分)
已知函數![]() .
.
(1)討論![]() 的單調性;
的單調性;
(2)若![]() 存在兩個極值點
存在兩個極值點![]() ,證明:
,證明:![]() .
.
(二)選考題:共10分。請考生在第22、23題中任選一題作答,如果多做,則按所做的第一題計分。
22.[選修4—4:坐標系與參數方程](10分)
在直角坐標系![]() 中,曲線
中,曲線![]() 的方程為
的方程為![]() .以坐標原點為極點,
.以坐標原點為極點,![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求![]() 的直角坐標方程;
的直角坐標方程;
(2)若![]() 與
與![]() 有且僅有三個公共點,求
有且僅有三個公共點,求![]() 的方程.
的方程.
23.[選修4—5:不等式選講](10分)
已知![]() .
.
(1)當![]() 時,求不等式
時,求不等式![]() 的解集;
的解集;
(2)若![]() 時不等式
時不等式![]() 成立,求
成立,求![]() 的取值范圍.
的取值范圍.






